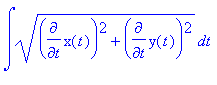Mathematica
The Flying Teacups
The material on these pages was adapted from
Calculus Projects Using Matheamtica, Copyright (c) 1992, 1993 and 1996 by
A. D. Andrew, G. L. Cain, S. S. Crum and T. D. Morley. Used with permission.
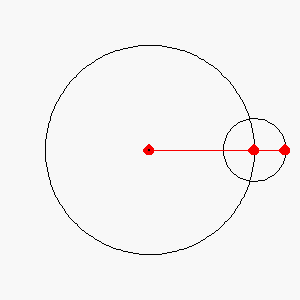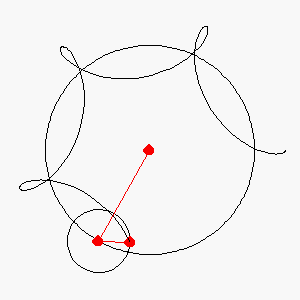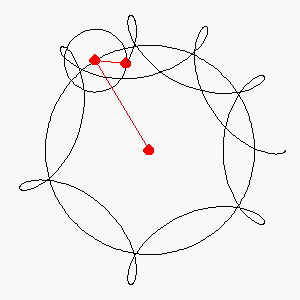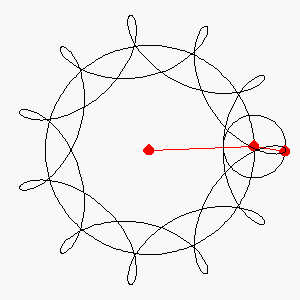
In this project you are asked to model the motion
of a famous carnival ride known as "The Flying Teacups". The
ride consists of four spokes at right angles to each other, each about
25 feet long, which rotate counterclockwise in a horizontal plane. At
the end of each spoke a disk of smaller radius is attached, and this disk
rotates clockwise about its center. Generally, the small disk appears
to have somewhat greater angular speed than does the imaginary disk of
long spokes.
The parametric equations for a circle are given
below. The variable r
is the
radius and the variable a
denotes the angular speed and direction of rotation.
x[t_]:= r Cos[a t]
y[t_]:= r Sin[a t]
r:=25
a:=1.5
ParametricPlot[{x[t],y[t]},{t,0,20},
AspectRatio->Automatic]
A set of parametric equations can be represented
in Mathematica
in the form of a vector.
g[t_]:={t,2t}
f[t_]:={Sin[2t],Sin[3t]}
The influence one curve has on another is very
curious.
Try to figure out how the following
curve is created from the above two curves.
Here is another set of parametric equations that may aid in the development
of the model.
x[t_]:= r Cos[a t]+r2 Cos[a2 t]
y[t_]:= r Sin[a t]+r2 Sin[a2 t]
a2:= -2.5
r2:= 10
ParametricPlot[{x[t],y[t]},{t,0,20},
AspectRatio->Automatic]
Here is the Mathematica
code for a description of the position
of a point 2 units inside a circle of radius r2 rotating inside along the
rim of a larger
circle of radius r1. The output is pretty interesting. This
type of curve is a modification
of the hypocycloid.
x1[t_]:={(r1+2-r2)Cos[t]+(r2+2) Cos[(r1+2-r2)
t/r2],
(r1+2-r2)Sin[t]-(r2+2) Sin[(r1+2-r2) t/r2]}
r1:=25
r2:=10
ParametricPlot[x1[t],{t,1,20}]
Once you have modeled the path of the ride,
you are asked to find the total length of the trip. The following is the
equation for the arclength of a Parametric curve. The limits on integration
are from t=0 to any time t. You should already know the Mathematica
code for integration. If you have forgotten just use the help functions.
Type ?Integrate for the proper syntax. Hint: try
to use vector properties to simplify the calculation since parametric curves
behave somewhat like vector equations.
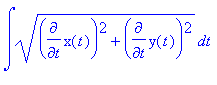
Vector
Equations
Index